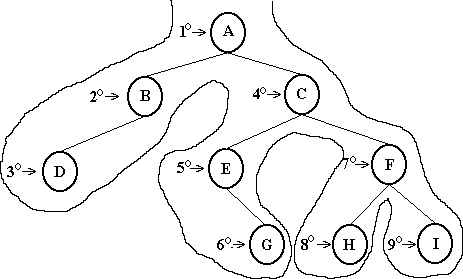

Pré-ordem:
Procedure PreOrdem(N:tree);
Begin
If N <> nil Then
Begin
Processa(N); {p. ex. imprime}
PreOrdem(N^.esq);
PreOrdem(N^.dir);
End;
End;
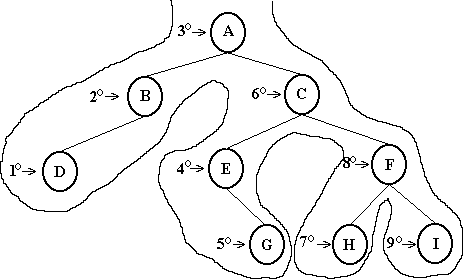
Procedure InOrdem(N:tree);
Begin
If N <> nil Then
Begin
InOrdem(N^.esq);
Processa(N); {p. ex: imprime}
InOrdem(N^.dir);
End;
End;
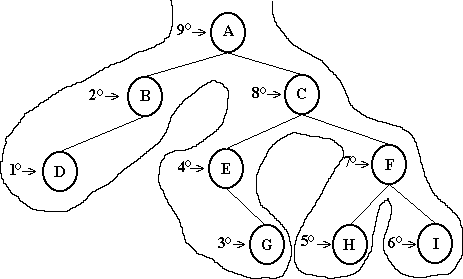
Procedure PosOrdem(N:tree)
Begin
If N <> nil Then
Begin
PosOrdem(N^.esq);
PosOrdem(N^.dir);
Processa(N); {p.ex.: imprime}
End;
End;
Function Esta_Presente(t: tree; item: Telem): boolean; Begin Esta_Presente:= busca(t, item) <> nil; End;
Function Busca(t:tree; item: Telem): Tree; Var achou: boolean; ptr: tree; Procedure Pós-Ordem(t:tree; var prt:tree; var achou:boolean); Begin If (t<>nil) and (not achou) then Begin Pós-Ordem(t^.esq,ptr,achou); if not achou then Pós-Ordem(t^.dir,ptr,achou);
If not achou then
If Igual(item, t^.info) Then
Begin
achou:=true;
ptr:=t;
End;
End;
End; {Pós-Ordem}
Begin {busca}
achou:=false;
ptr:=nil;
Pós-Ordem(t,ptr,achou);
busca:=ptr;
End; {busca}
Outra versão para busca
Function Busca1(t: tree; item: Telem): tree;
Var achou:boolean;
Function Local(t: tree; item: Telem; var achou:boolean):tree;
Begin
If not vazia (t) then
If t^.info=item then local:=t;
Else
Begin
local:=local(t^.esq, item, achou);
If not achou Then
local=local(t^.dir, item, achou);
End;
End; {local}
Begin {busca1}
busca1:= nil;
busca1:=local(t, item, achou); End;Tornar uma árvore vazia
Procedure Tornar_Vazia(var t: tree); Begin If not Vazia(t) Then Begin Tornar_Vazia(t^.esq); Tornar_Vazia(t^.dir); Dispose(t); End; t:=nil; End;Treinar o rastreamento dos Algoritmos de Travessia em Árvore Binária.