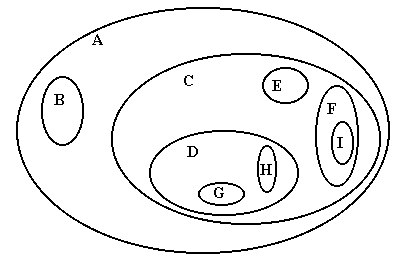
Representação por parênteses aninhados
( A (B) ( C (D (G) (H)) (E) (F (I)) ) )Diagrama de inclusão

Representação hierárquica
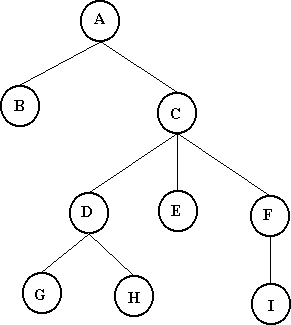
A subárvore Tc possui 3 subárvores:
Td, Tf e Te onde
Td = {D, G, H}
Tf = {F, I}
Te = {E}
As subárvores Tb, Te, Tg, Th, Ti possuem apenas o nó raiz e nenhuma subárvore.
Exemplo: representação da expressão aritmética: (a + (b * (c / d) - e))
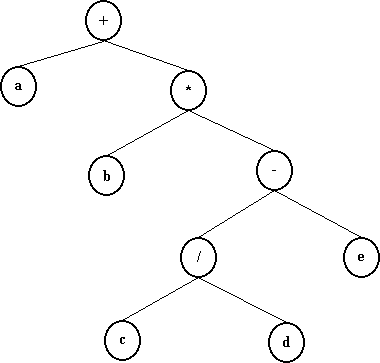
Nós filhos, pais, tios, irmãos e avô
Seja v o nó raiz da subárvore Tv de T.
Os nós raízes w1, w2, ... wj das subárvores de
Tv são chamados filhos de v.
v é chamado pai de w1, w2, ... wj.
Os nós w1, w2, ...wj são irmãos.
Se z é filho de w1 então w2 é tio de z e v é
avô de z.
Grau de saída, descendente e ancestral
O número de filhos de um nó é chamado grau de saída
desse nó.
Se x pertence à subárvore Tv, então, x é
descendente de v e v é ancestral, ou antecessor, de x. Se neste
caso x é diferente de v então x é descendente próprio
de v e v é ancestral próprio de x.
Nó folha e nó interior
Um nó que não possui descendentes próprios é
chamado de nó folha, ou seja, um nó folha é aquele
com grau de saída nulo.
Um nó que não é folha (isto é, possui grau
de saída diferente de zero) é chamado nó interior
ou nó interno.
Grau de uma árvore
O grau de uma árvore é o máximo entre os graus de seus nós.
Floresta
Uma floresta é um conjunto de zero ou mais árvores.
Caminho, comprimento do caminho
Uma sequência de nós distintos v1, v2, ..., vk, tal que
existe sempre entre nós consecutivos ( isto é, entre v1 e
v2, entre v2 e v3, ... , v(k-1) e vk) a relação "é
filho de"ou "é pai de" é denominada um caminho na árvore.
Diz-se que v1 alcança vk e que vk é alcançado
por v1.
Um caminho de vk vértices é obtido pela sequência
de k-1 pares. O valor k-1 é o comprimento do caminho.
Nível (ou profundidade) e altura de um nó
O nível ou profundidade, de um nó é o número
de nós do caminho da raiz até o nó.
O nível da raiz, é portanto, 1.
A altura de um nó v é o número de nós no
maior caminho de v até um de seus descendentes.
As folhas têm altura 1.
Nível da raiz (profundidade) e altura de uma árvore
O nível da raiz é 1 (acima). A altura de uma árvore T é igual ao máximo nivel de seus nós. Representa-se a altura de T por h(T) e a altura da subárvore de raiz v por h(v).
Árvore Ordenada
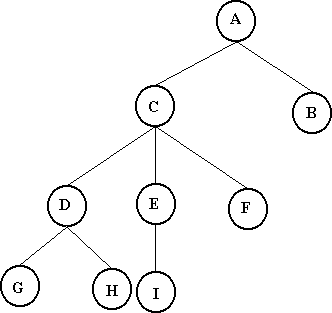
Uma árvore ordenada é aquela na qual os filhos de cada nó estão ordenados. Assume-se ordenação da esquerda para a direita. Desse modo a árvore do primeiro exemplo é ordenada, mas, a árvore abaixo não.
Árvores Isomórfas
Duas árvores não ordenadas são isomórfas quando puderem se tornar coincidentes através de uma permutação na ordem das subárvores de seus nós. Duas árvores ordenadas são isomórfas quando forem coincidentes segundo a ordenação existente entre seus nós.
Árvore Cheia
Uma árvore de grau d é uma árvore cheia se possui o número máximo de nós, isto é, todos os nós tem número máximo de filhos exceto as folhas, e todas as folhas estão na mesma altura.
Árvore cheia de grau 2: implementação sequencial.
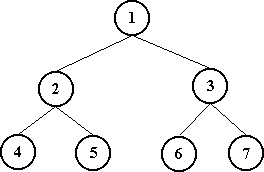
Array com 7 posições:

Armazenamento por nível:
posição do nó posição dos filhos do nó 1 2,3 2 4,5 3 6,7 i (2i,2i+1)Dentre as árvores, as binárias são, sem dúvida, as mais comumente utilizadas nas aplicações em computação.