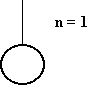
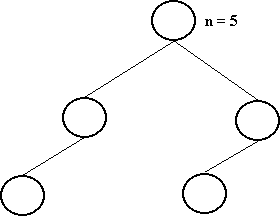
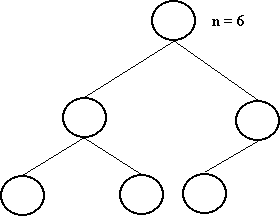
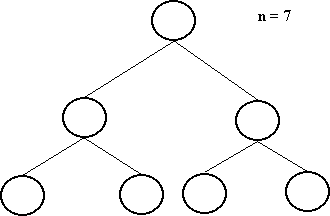
Uma árvore binária é dita balanceada se, para cada nó, as alturas de suas subárvores diferem de, no máximo 1.

Árvore Binária Perfeitamente Balanceada

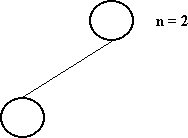
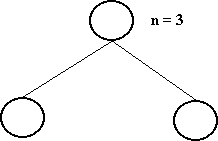
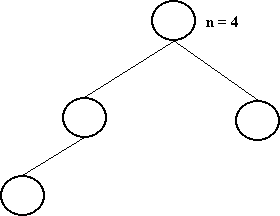
Uma árvore binária é dita perfeitamente balanceada se, para cada nó, o número de nós de suas subárvores diferem de no máximo, 1.

Altura de Árvore Perfeitamente Balanceada

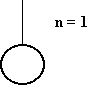
Árvore Perfeitamente Balanceada é a árvore com menor altura para o seu número de nós.

Procedimento recursivo para geração balanceada de nós:

1. Use um nó para a raiz.
2. Gere a subárvore esquerda com nl = n div 2 nós, usando este mesmo procedimento.
3. Gere a subárvore direita com nr = n - nl - 1 nós, usando este mesmo procedimento.

  Program Buildtree(input, output);
  Type ref = ^ node;
       node = record
                key:integer;
                left, right: ref;
              End;

  Var n: integer;
      root: ref;

  Function tree(n: integer): ref;
  Var newnode: ref;
      x, nl, nr: integer;

  Begin
    If n=0 Then
      tree:=nil;
    Else
      Begin
        nl:=n div 2;
        nr:=n - nl -1;
        read(x);  { conteúdo do nó }
        new (newnode);
        with newnode^ do
          Begin
            key:=x;
            left:=tree(nl);
            right:=tree(nr);
          End;
        tree:=newnode;
      End;
  End; {tree}

    Duas possibilidades: in-order (versão em verde)

                         in-order "invertido" (isto é, caminhando à direita primeiro)

                                    (versão em vermelho)

  Procedure Printtree(t: ref; h: integer);
  Var i: integer;
  {pre-condição: h deve ser a altura da árvore}

  {pre-condição: h deve ser a distância da margem ao primeiro elemento impresso}
  Begin {imprime tree t com indentação h}
    If t<>nil Then
      with t^ do
        Begin
          printtree(left, h-1); printtree(right, h+1);
          for i:=1 to h do 
            write('     ');
          writeln(key);
          printtree(right, h-1);printtree(right, h+1);
       End;
  End;    {printtree);


  Begin                         {buildtree: programa principal}
    read(n);                    { primeiro inteiro especIfica número de nós }
    root:=tree(n);
    printtree(root, h(root));   {h é a função que determina a altura da árvore}
  End;  { buildtree}

-> Exercício: re-escrever o print-tree para imprimir a árvore em pé, fazendo a

travessia por níveis.

Rebalanceamento de Árvores

Índice