Árvore AVL:

Uma árvore AVL é uma árvore binária de busca (ABB) construída de tal modo que a altura de sua subárvore direita difere da altura da subárvore esquerda de no máximo 1.

Inserção AVL:

O que pode acontecer quando um novo nó é inserido numa árvore balanceada ?

Dada uma raiz r com subárvores L (left) e R (right), e supondo que a inserção deve ser feita na sub-árvore da esquerda. Podemos distriguir 3 casos:

1. Se hL = hR, então L e R ficam com alturas diferentes mas continuam balanceadas.
2. Se hL < hR, então L e R ficam com alturas iguais e balanceamento foi melhorado.
3. Se hL > hR, então L fica ainda maior e balanceamento foi violado.

• Nós 9 ou 11 podem ser inseridos sem balanaceamento . Subárvore com raiz 10 passa a ter uma subárvore e subárvore com raiz 8 vai ficar melhor balanceada !
• Inserção dos nós 3, 5 ou 7 requerem que a árvore seja rebalanceada!

É a altura da subárvore direita do nó menos a altura da subárvore esquerda do nó

Rebalanceamento:

Os problemas podem ser mapeados para dois casos:

Tipo 1: o nó raiz de uma subárvore tem FB 2 (ou -2) e tem um filho com FB 1 (-1) o qual tem o mesmo sinal que o FB do nó pai. Exemplos:
 
Exemplo 1:                                            Exemplo 2:

• solução: rotação simples sobre o nó de FB=2 (-2).
• Rotações são feitas à esquerda quando FB positivo e à direita quando FB negativo.

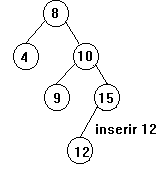
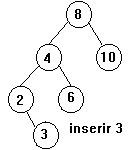
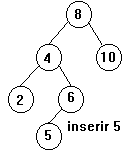
-> De acordo com o demonstrado em sala de aula, fazer as rotações adequadas para o re-balanceamento das árvores dos exemplos 1 e 2 acima.
 

   procedure rotacao_direita (Var p:pno); 
   Var q, temp: pno;
   begin
     q  = esq(p);
     temp = dir(q);
     dir(q) =  p;
     esq(p) = temp;
   end;

rotação_esquerda(p)

   procedure rotacao_esquerda(Var p: pno;);
   Var q, temp: pno;
   begin  
     q  = dir(p);
     temp  = esq(q);
     esq(q) = p;
     dir(p) = temp;
   end;

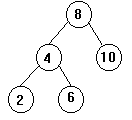
Tipo 2: o nó raiz de uma subárvore tem FB=2 (ou -2) e tem uma um filho com FB=-1 (1) o qual tem o sinal oposto ao FB do nó pai.

Exemplo: Caso (-2) (1)
FB do nó que contém 8: -2
FB do nó que contém 4: 1

• solução: duas rotações
1. primeiro roda-se o nó com FB=1 (-1) na direção apropriada
2. depois roda-se o nó que tinha FB=-2 (2) na direção oposta

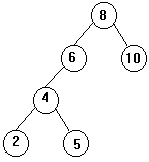
Rotação de 8 à direita

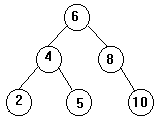
-> Elaborar um caso (2) (-1) e executar o re-balanceamento.

-> Re-fazer os algoritmos de rotação à esquerda e à direita, considerando o caso geral de re-balanceamento de sub-árvores, utilizando a definição inicial de árvora binária (tree).

Árvore Binária

Índice