1. Todas as chaves da subárvore esquerda são menores que a chave da raiz.
2. Todas as chaves da subárvore direita são maiores que a chave raiz.
3. As subárvores direita e esquerda são também Árvores Binárias de Busca.

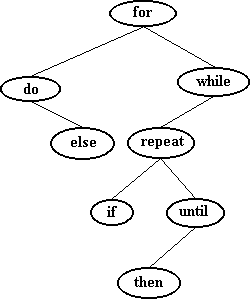
Em algoritmo de busca a medida de eficiência é dada pelo número de comparações necessárias para se localizar uma chave, ou descobrir que ela não existe.

Numa lista linear com n chaves, temos que, no pior caso, faremos n comparações. O número de comparações cresce linearmente em função do número de chaves.

Busca binária

Pesquisa realizada se informação está armazenada de forma ordenada e em sequência (em um array).

Qual a eficiência do Algoritmo de busca binária ?

• Para n = 8 posições, o pior caso é quando precisando chegar na posição 1 ou 8.
• A cada divisão, desprezamos toda a porção maior ou menor que a chave.

            1                                        n/2
            2                                        n/4
           k                                        n/2^{k
            i                                          1}
 
       n/2ⁱ = 1  =>   n = 2ⁱ   =>   i = log₂n
 

Com busca binária obtemos a melhor eficiência possível em array, mas, ficamos limitados à representação sequencial (deslocamentos, previsão de memória, etc).

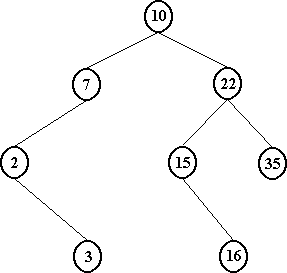
Podemos utilizar a Árvore Binária de Busca e obteremos o mesmo desempenho anterior - desde que a altura seja mínima. É a característica de altura mínima que garante que estamos tomando a chave do meio da porção pesquisada !!

Com Árvore Binária de Busca Perfeitamente Balanceadas temos altura mínima.
O número de comparações será igual a :

Para garantir a performance ótima temos que garantir que a árvore seja balanceada durante a construção e que o balanceamento seja mantido em inserções e eliminações !

Definição da Estrutura de Dados e Algoritmos:

  Type Pno=^No;
       Tree = Pno;
       No=record
            chave: Tchave;
            esq, dir: Pno;
          End;

  Var raiz: Tree;

  Function Busca (x: Tchave; raiz: Tree;):Tree;
  Var achou: boolean;
      p: Tree;

  Begin
    p:=raiz;
    achou:=false;
    While (not achou) and (p<>nil) do
      If p^.chave = x Then
        achou:=true
      Else
        If p^.chave > x Then 
          p:=p^.esq
        Else p:=p^.dir;
    Busca:=p;
  End;

  Function Busca (x: Tchave; raiz: Tree;):Tree;
  Begin
    If raiz=nil Then 
      Busca = nil
    Else 
      If raiz^.chave = x Then 
        busca:=raiz
      Else 
        If raiz^.chave < x Then 
         Busca:=Busca(x, raiz^.dir)
        Else
          Busca:=Busca(x,raiz^.esq);
  End;

  Function Busca (x: Tchave; raiz: Tree):Tree;
  Var sentinela,
      p: Tree;

  Begin
    p:=raiz;
    sentinela^.chave:=x;
    While p^.chave <> x do
      If p^.chave x Then 
        p:=p^.dir
      Else p:=p^.esq;
    Busca:=p;
  End;