Inserção e eliminação na mesma extremidade

Caso 1: Duas Pilhas

Em vez de A1[1..m1] e A2[1..M2], faz-se A[1..M], M maior ou igual a M1+M2.

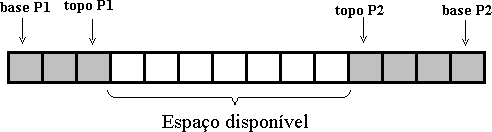
Consequências:

• overflow ocorre apenas se o número total de elementos de ambas as pilhas exceder M (ou seja: topoP1 = topoP2-1)
• base de cada pilha fica numa posição determinada na inicialização:

topoP1:=0 {cresce para a direita}
topoP2:=M+1 {cresce para a esquerda}

• Quando mais de duas pilhas são alocadas no mesmo array, não é mais possível deixar as bases de cada pilha fixadas.

Sejam as pilhas i tais que:

• Base i aponta o registro anterior ao primeiro elemento da pilha
• Topo i aponta o último elemento armazenado
• Pilha i vazia - Topo i = Base i
• Pilha i cheia - Topo i = Base (i+1)

  type pilha_m: array[1..m] of Tipoelem;
       ind: array[1..n] of indice;
 
  var A: pilha_m;
      topo, base: ind;

Push i
{ inserção na pilha i}

  procedure push (Var A: pilha_m; topo, base: ind; x:TipoElem, i: integer);
  begin
    if topo[i]=base[i+1] then {Overflow}
    else
      begin
        topo[i]:=topo[i]+1;
        A[topo[i]]:=x;
      end;
  end;

• utiliza-se uma pilha fictícia n+1
• com base[n+1] = m

  procedure elimina (Var topo, base:ind);
  begin
    if topo[i]=base[i] then {underflow}
    else
      topo[i]:=topo[i-1];
  end;

A condição de overflow na inserção pode ser adiada se o vetor A tiver algum espaço vazio para uma pilha j, o qual pode ser cedido à pilha i.

Alternativas

• procura-se uma pilha k acima da pilha i, i< k < = n, tal que topo[k] < base[k+1] e desloca-se de uma posição as pilhas compreendidas entre i+1 e k inclusive.
• procura-se uma pilha k abaixo de i, 1<=k<i tal que base[k]>topo[k+1] e desloca-se as pilhas compreendidas entre k e i, inclusive.

O que ocorre se inicializarmos

• topo[i] = 0
• base[i] = 0, i=1..n

Solução: inicialização equilibrada - dividir proporcionalmente os m registros entre as n pilhas.

Pilha